PID Control#

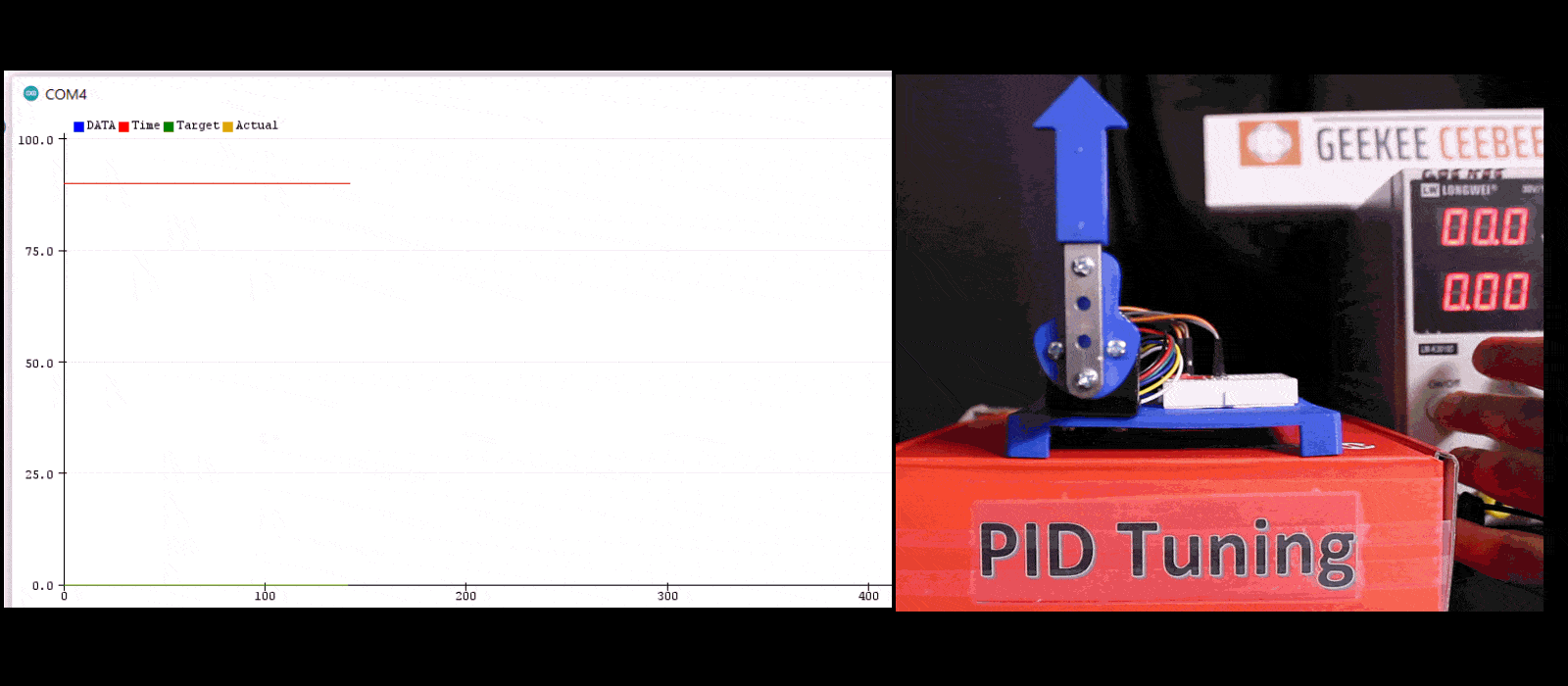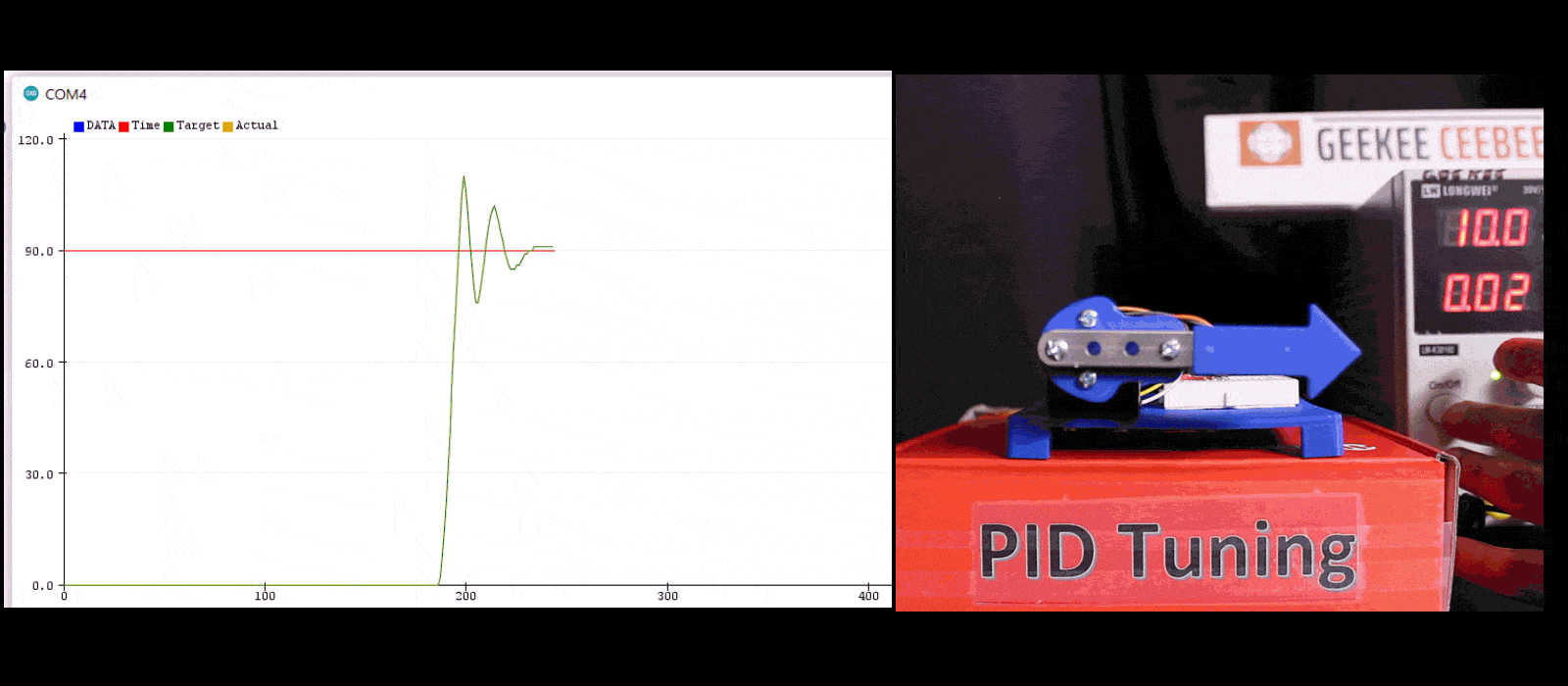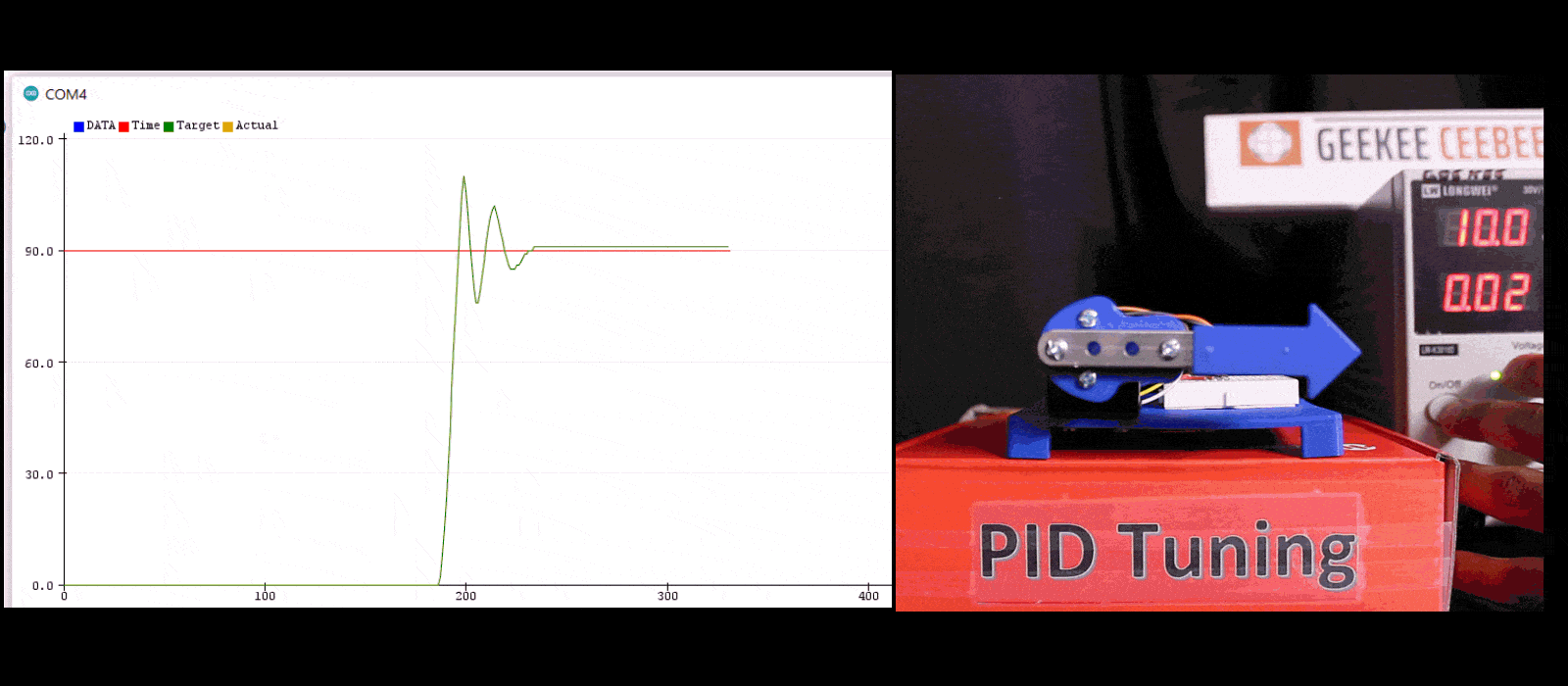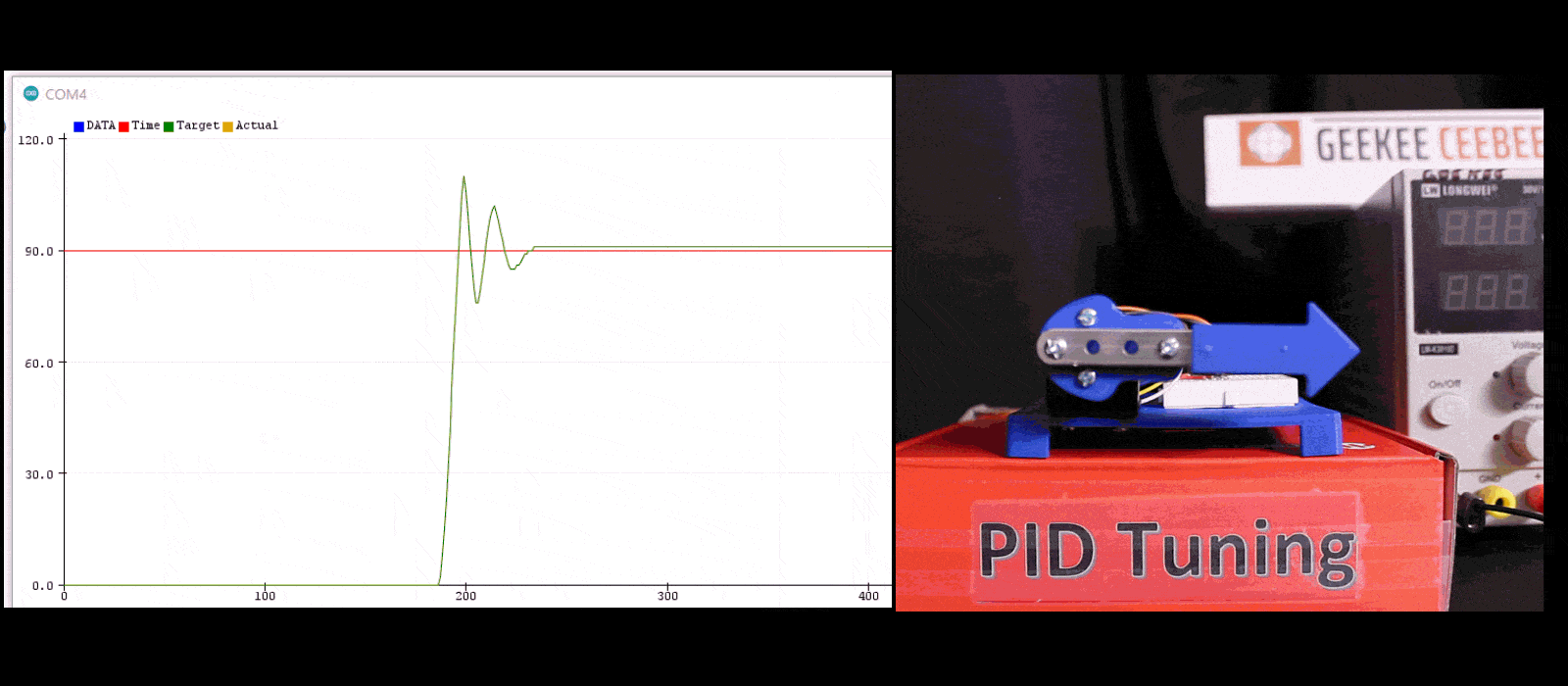
PID (Proportional-Integral-Derivative) control is a widely used feedback control algorithm in engineering. It plays a crucial role in maintaining desired setpoints or target values in various systems like motors, including robotics.

PID control is a closed-loop control technique that uses feedback from the system to control the process. It continuously calculates an error value as the difference between a desired setpoint and a measured process variable and applies a correction based on proportional, integral, and derivative terms. The goal is to minimize the error and achieve the desired setpoint as quickly as possible.

PID control is used in a wide range of applications, including robotics, manufacturing, and process control. It is also used in many First Robotics competitions to control various robot functions like motor speed, shooter velocity, and autonomous navigation.

Why do we need PID control?#

PID control is a popular control technique because it is simple, robust, and effective. It is easy to implement and can be used to control a wide range of systems. It is also very reliable and can handle various disturbances and uncertainties in the system. Finally, it is very effective at minimizing the error and achieving the desired setpoint quickly.

If PID control was not used in robotics, the robot would not be able to maintain a consistent speed or position and would not be able to perform precise movements, as different external factors would affect the robot’s behavior, like friction, gravity, or other disturbances.

We use PID control in robotics to achieve consistent, presise, and smooth movements, which is crucial for mechanisms that can be easily damaged or require precise control, like arm mechanisms or shooter systems.

Use of PID in First Robotics#

First Robotics competitions often rely on PID controllers for precise control of various robot functions. Here’s how PID control is utilized:

Motor Control: PID loops can control motor speed or position to achieve consistent robot movements or maintain specific arm or shooter positions.
Shooter Systems: PID controllers are used to precisely control shooter velocity and angle for accurate object launching.
Autonomous Navigation: PID control helps the robot navigate to specific positions or follow predefined paths accurately, especially in autonomous modes.
Stability and Balance: In situations where robots need to balance on platforms or manipulate objects delicately, PID control ensures stability and precise control.

PID Control Theory#

Proportional (P):#

The proportional term in a PID controller produces an output value that is proportional to the current error. It results in a control response that reduces the error by a certain factor. Increasing the proportional gain can make the system respond more aggressively but may lead to overshooting the setpoint.

Integral (I):#

The integral term accounts for past errors by summing up the error values over time and applying a correction based on the accumulated error. It eliminates any residual steady-state error and helps the system reach the setpoint accurately.

Derivative (D):#

The derivative term anticipates future error by calculating the rate of change of the error over time. It provides a control response to counteract rapid changes in error, preventing overshoot and oscillations.

feed-forward (FF):#

feed-forward is a term that is added to the PID controller to compensate for external forces acting on the system, like friction or gravity. It is used to improve the system’s response and achieve the desired setpoint more quickly.

Creating PID Control for FIRST Robotics#

Find your feedback sensor#

The first step in creating a PID controller is to find a sensor that can provide feedback about the system’s current state. The sensor should be able to measure the process variable (PV) or the system’s current state and provide feedback to the controller. The sensor can be a potentiometer, encoder, or any other device that can measure the system’s current state.

Find your setpoint#

The setpoint is the desired value that the system should achieve. It can be a specific position, speed, or any other value that the system needs to maintain. The setpoint can be a constant value or a variable that changes over time.

Find your control output#

The control output is the value that the PID controller calculates and sends to the system to achieve the desired setpoint. It can be a voltage, current, or any other value that the system can use to control the process.

Note

The control output should be within the system’s operating range. For example, if the system uses a motor, the control output should be a voltage or current that the motor can handle. It also needs to be within the sensor’s measurement range. For example, if the sensor is a potentiometer, the control output should be a voltage that the potentiometer can measure. Finally, it needs to be within the systems’ physical limits. For example, if the system is a robot arm, the control output should be a position that the arm can reach, otherwise the arm will be damaged.

Use the PID controller class from the wpilib library#

Here is the class and helpful methods that can be used to create a PID controller in Python:

from wpilib import PIDController

pid = PIDController(0.1, 0.01, 0.001) # WPIlib PID Controller Class - Takes in P, I, and D values

pid.setSetpoint(10) # Set the desired setpoint

pid.enable() # Enable the PID controller

pid.disable() # Disable the PID controller

pid.reset() # Reset the PID controller to its initial state - Very important to call this before restarting a Command, otherwise the PID controller will continue from the previous Command

pid.getSetpoint() # Get the current setpoint

Calculate the error and set the output#

setpoint = 10 # Set the desired setpoint

output = pid.calculate(sensor.get(), setpoint) # Calculate the PID output based on the current sensor value

motor.set(output) # Set the motor output to the PID output

Repeat the above step in a loop to continuously calculate the PID output and set the motor output.

Tuning the PID Controller#

Tuning is the process of adjusting the PID controller’s parameters to achieve the desired response.

The PID controller has three parameters: the proportional gain, the integral gain, and the derivative gain.

Important

It may also be necessary to add a feed-forward term to the PID controller to compensate for external forces acting on the system, like friction or gravity.

Not all PID controllers use all three parameters. Some PID controllers only use the proportional and Derivative gain, while others use all three parameters. In FIRST Robotics, it is rare to use the integral gain, as it can cause the system to overshoot the setpoint and oscillate around it.

Identify whether the system is affected by a constant external force, like gravity or friction. If so, add a feed-forward term to the PID controller to compensate for the external force. This value should be a number that is right before the system starts moving. For example, if the system starts moving at 0.1 volts, the feed-forward term should be 0.1 volts. .. important:
```
If your external force is something like gravity, you may need to use a negative feed-forward term to compensate for the force when traveling in the opposite direction.
```
Set the integral gain to 0 and the derivative gain to 0. This will make the PID controller act like a proportional controller, which is the simplest type of controller.
Increase the proportional gain until the system starts to oscillate around the setpoint. This is called the critical gain. The critical gain is the gain at which the system starts to oscillate.
Increase the derivative gain until the system stops oscillating and reaches the setpoint quickly. This is called the critical damping. The critical damping is the gain at which the system stops oscillating.
This may be enough to achieve the desired response. If not, increase the integral gain until the system reaches the setpoint accurately. This is called the critical integral gain. The critical integral gain is the gain at which the system reaches the setpoint accurately.

Important

Some PID controllers may work under different conditions, like when the system is moving or when the setpoint is changing. It is important to test the PID controller under different conditions to ensure that it works properly.

Troubleshooting PID Control#

Note

If the system is not responding to the PID controller, check the following:

Make sure that the sensor is connected properly and is working correctly.
Make sure that the control output is within the system’s operating range and is traveling in the correct direction.
Make sure that the control output is within the sensor’s measurement range.
Make sure that the control output is within the system’s physical limits.